We may input a graph on a computer by its Adjacency Matrix or Adjacency List. Essentially speaking, these two methods are equivalent, so I would like to introduce you the adjacency matrix only.

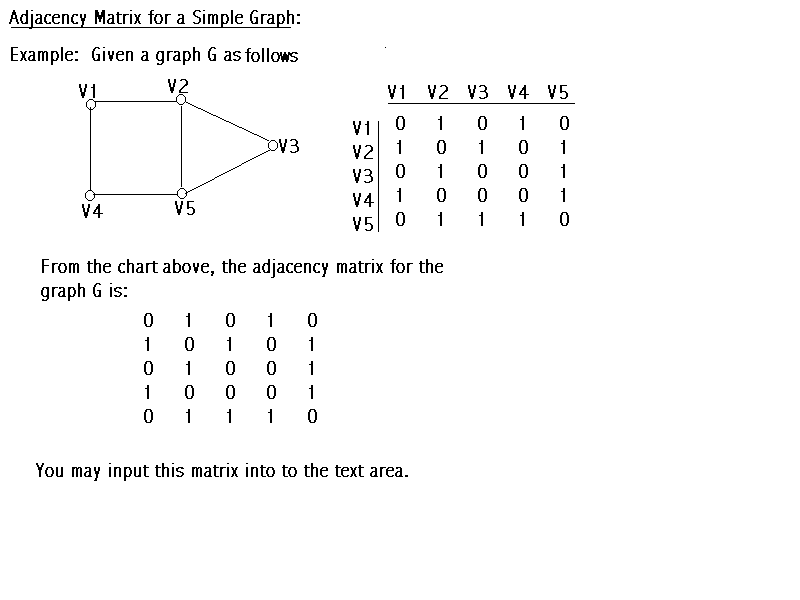
• To construct the adjacency matrix for a Simple Graph , one can label all the vertices in order. Assume that there are p vertices, we name them as V1, V2, V3, ..., Vp. Consider a block of numbers, called a matrix, with p rows, representing the p vertices in order, and p columns, representing the same p vertices in order.   If Vi is adjacent to Vj, then place 1 at the ith row and jth column and 1 at jth row and ith column; place 0 otherwise. When you input this adjacency matrix into the text area, do not include the vertex names, only input the numbers.  The adjacency matrix is symmetric for a simple graph.

  

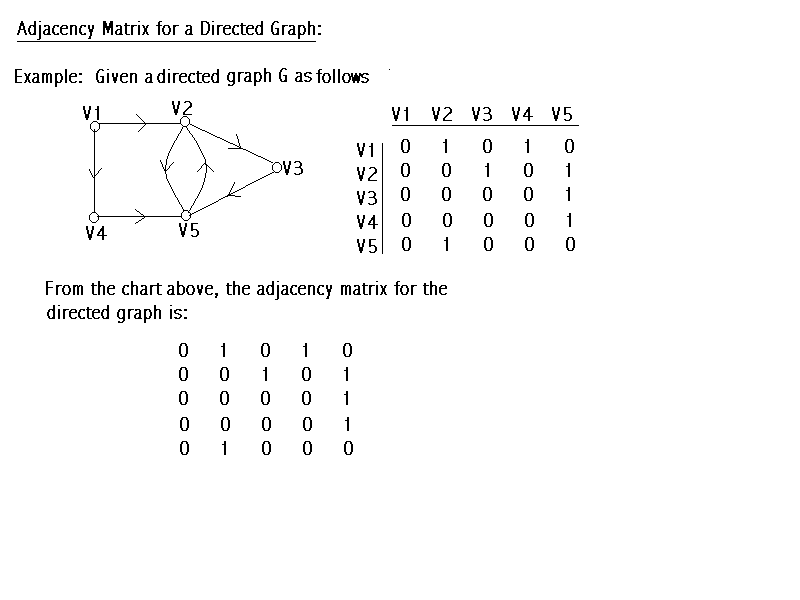
• If we have a Directed Graph, we may construct the adjacency matrix the same way. But, for each directed edge (Vi, Vj), we place 1 at ith row and jth column, 0 at jth row and ith column except that there is another directed edge (Vj, Vi).   the adjacency matrix, in general, is not symmetric for a directed graph.

  

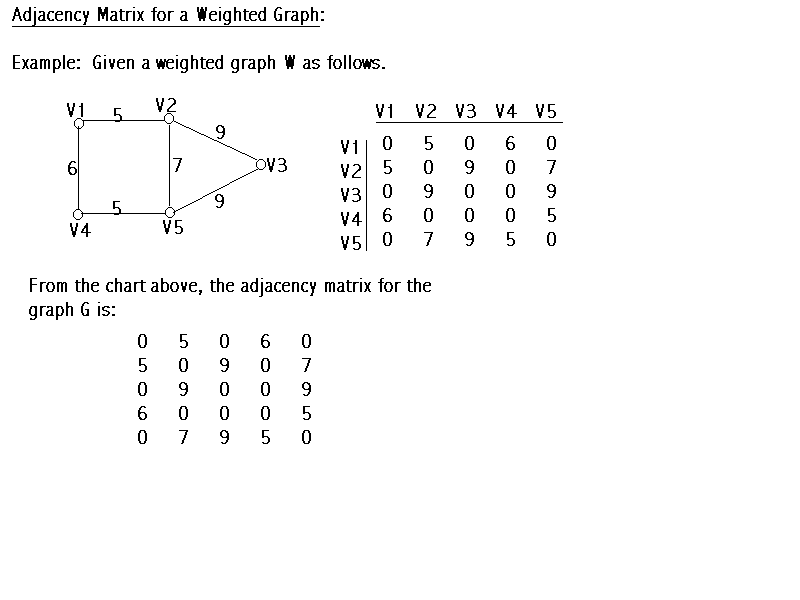
• If we have a Weighted Graph, again, we may construct the adjacency matrix the same way. But, for two adjacent vertices Vi and Vj, we place the weight value at ith row and jth column in stead of 1 (also place the weight at jth row and ith column).   Then, follow the same rule for a simple graph.  the adjacency matrix is symmetric for a weighted graph, too.

  

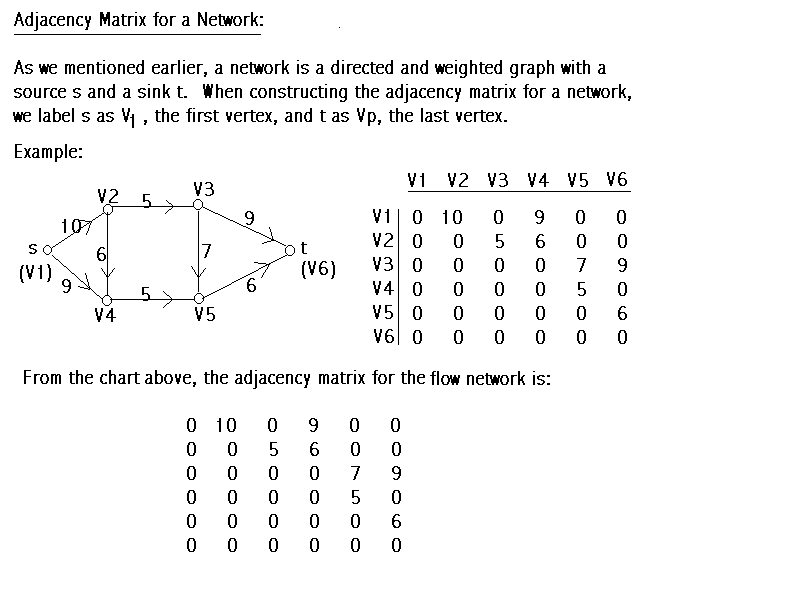
• Finally, let's construct the adjacency matrix for a Flow Network.  A flow network is a directed and weighted graph with a source s and a sink t. Label the source s as the first vertex and label t as the last vertex. Then, follow the rule for directed and weighted graph.